개요
요즘 자연로그($ln$)가 자주 보여서 알아두면 평생 쓰겠다 싶어 공부시작.
자연로그를 알려면 자연상수 e를 알아야한단다.
자연상수 e를 알려면 적분을 알아야하고, 적분을 알려면 미분을 알아야하고,
미분을 하려면 극한을 알아야한단다 ㅡㅡ
그래서 그냥 이것저것 모르는 것들은 배우면서 자연상수 $e$를 유도해 보았다.
$e$ 의 정의
일단 이자가 100%인 경우가 있다고 생각해보자.
이 경우에는 원금 1원을 넣으면 1년 후 2원이 된다.
만약 여기서 6개월마다 이자를 복리로 받는다면 어떻게 될까?
원금 1원을 넣고 6개월 후 이자로 0.5원을 받는다.
이자를 포함한 1.5원을 다시 넣어두면 6개월 후에는 2.25원이 된다.
그렇다면 3개월마다 이자를 복리로 받는다면 어떻게 될까?
혹은 1일마다 이자를 복리로 받는다면?
이런식으로 이자를 받는 간격을 무한히 줄이면 받는 돈이 무한히 많아지는 것은 아니고,
어떠한 값에 수렴한다.
이를 자연상수 $e$라고 정의한다.
유도 과정
일단 이를 식으로 표현해보자.
원금 1원에 이자를 1년에 동일한 간격으로 무한히 많은 $n$번 받는다고 하자.
$ \large e = \lim\limits_{n \to \infty} (1 + \frac{1}{n})^n $
이게 e의 정의이다.
하지만 제대로 이해하기 위해서 이를 함수 그래프로 생각해보자.
$\bf {f(x) = 1}$
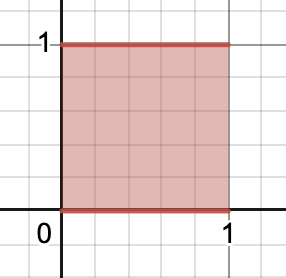
원금에 대한 그래프는 위와 같이 상수 함수로 표현할 수 있다.
그리고 이 원금에 대한 이자는 이 그래프의 넓이를 구하는 식으로 표현할 수 있을 것이다.
$\bf {y = x}$
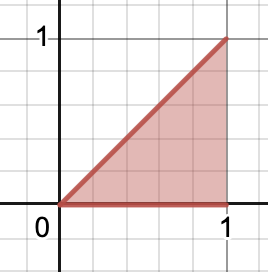
y = 1 그래프를 아주 잘게 쪼갠다면 x가 증가할 때마다 넓이가 x만큼 증가한다고 볼 수 있으므로
넓이에 대한 그래프는 y = x로 표현할 수 있다.
1년에 한 번 이자를 받는다면 위 그래프대로 1,
6개월에 받는다면 0.5x 시점인 0.5를 받을 것이다.
여기서, 복리는 이 1차적인 이자에 대한 이자를 받는 것이므로,
이 그래프의 넓이에 대한 식을 구하면 이 이자에 대한 이자의 그래프가 될 것이다.
그래프의 넓이는 삼각형이므로 $y = \frac{x^2}{2}$로 표현할 수 있다.
$\bf {y = \frac{x^2}{2}}$
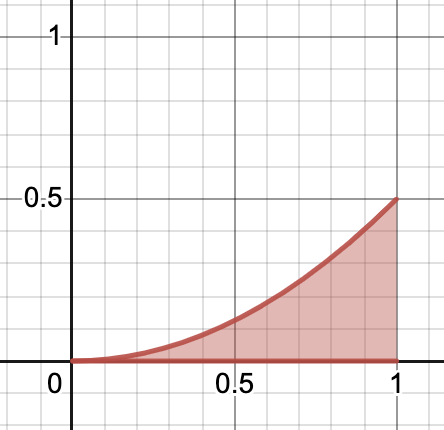
위 함수로 이자에 대한 이자를 표현할 수 있다.
이런식으로 이자에 대한 이자, 이자에 대한 이자에 대한 이자… 를 무한히 반복하여 이자에 대한 함수를 구하고
모두 더하면 e 에 수렴하는 값이 나올 것이다.
$e = 1 + 1 + \frac{x}{1} + \frac{x^2}{2} + … $
이자 그래프의 넓이 구하기
아까 구한 $y = \frac{x^2}{2}$ 이자에 대한 이자를 또 구하려면
그래프의 넓이를 구하면 되는데, 이제 단순한 삼각형이 아니므로 넓이를 곧바로 구할 수 없다.
$\bf {y = \frac{x^2}{2}}$

위 그래프의 넓이를 구하기 위해 무수히 쪼갠다는 아이디어를 사용한다.(극한(?))
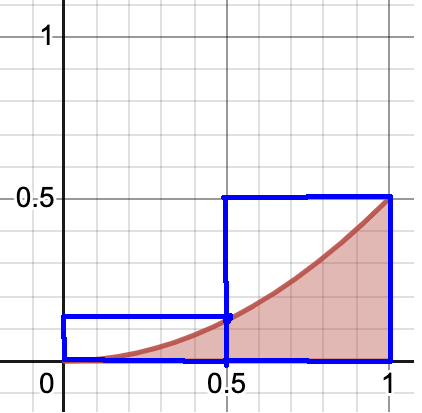
일단 해당 그래프를 절반으로 쪼개어 넓이를 구해보자.
두 개의 직사각형에 대한 넓이를 구하는 것이다.
물론 두 직사각형의 넓이는 그래프의 넓이와 오차가 크지만,
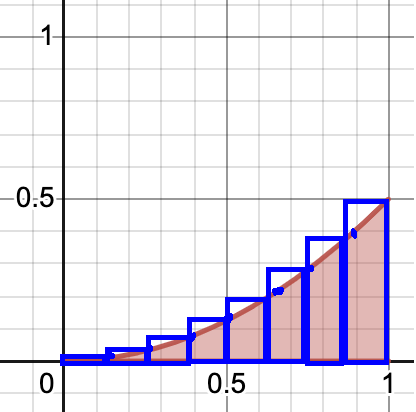
무수히 많이 쪼개면 그래프의 넓이에 근사할 것이다.
그렇다면 이를 식으로 표현해보자.
그래프를 직사각형 $n$개로 무수히 쪼개어 넓이를 모두 더한다.
직사각형의 가로는 $\frac{x}{n}$이고, 세로는 그래프 식 $\frac{x^2}{2}$에 직사각형의 끝 $x$좌표인 $k \cdot \frac{x}{n}$를 대입한 값이다.
$
\lim\limits_{n \to \infty} \ \sum\limits_{k=1}^{n} [ \frac{x}{n} \cdot \frac{(k \frac{x}{n})^2}{2} ]
$
$
\lim\limits_{n \to \infty} \ \sum\limits_{k=1}^{n} [ \frac{x}{n} \cdot k^2 \cdot \frac{x^2}{n^2} \cdot \frac{1}{2} ]
$
$
\lim\limits_{n \to \infty} \ \sum\limits_{k=1}^{n} [ \frac{x^3}{2n^3} \cdot k^2 ]
$
$
\lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \sum\limits_{k=1}^{n} k^2
$
이제 $\sum\limits_{k=1}^{n} k^2$를 구해야 하는데,
$\sum\limits_{k=1}^{n} k$ 처럼 가우스 합으로 바로 구할 수 없으므로 유도해보자…
$\sum\limits_{k=1}^{n} k^2$ 풀기
일단 $\sum\limits_{k=1}^{n} k^2$는 3차식으로 표현할 수 있을 것이다.
그래서 $\sum\limits_{k=1}^{n} k^3$ 형식에서 유도할 것.
Telescope sum을 사용한다.
$\sum\limits_{i=0}^{k} [(i + 1)^3 - i^3]$
이 식을 주르륵 다 적어보자.
$1^3 - 0^3 +$
$2^3 - 1^3 +$
$3^3 - 2^3 +$
$4^3 - 3^3 +$
$…$
$(k + 1)^3 - k^3$
최종적으로 서로 상쇄되어 남은 $(k + 1)^3$ 이 나온다.
그러므로
$\sum\limits_{i=0}^{k} [(i + 1)^3 - i^3] = (k + 1)^3$
그리고 여기서 $(i + 3)^3 - i^3 = 3i^2 + 3i + 1$ 이므로, 다음과 같이 치환할 수 있다.
$ \sum\limits_{i=0}^{k} [(i + 1)^3 - i^3] = 3\sum\limits_{i=0}^{k} i^2 + 3\sum\limits_{i=0}^{k} i + \sum\limits_{i=0}^{k} 1 = (k + 1)^3 $
$\sum\limits_{i=0}^{k} i$ 는 가우스 합으로 $\frac{k(k + 1)}{2}$ 가 되고,
$\sum\limits_{i=0}^{k} 1$ 은 $k + 1$ 이다.
$\sum\limits_{i=0}^{k} i^2$ 는 모르므로 이를 좌변에 두고 나머지를 우변으로 옮기면,
$\sum\limits_{i=0}^{k} i^2 = \frac{1}{3}[(k + 1)^3 - \frac{3k(k + 1)}{2} - (k + 1)]$ 이다.
하지만 우리가 최종적으로 원하는 것은
$\sum\limits_{i=0}^{k}$ 꼴이 아닌 $\sum\limits_{i=1}^{k}$ 꼴이므로 문제가 생길 수 있는데,
$\sum\limits_{i=0}^{k} i^2$, $\sum\limits_{i=0}^{k} i$ 는 0을 대입하면 어차피 0이므로 $\sum\limits_{i=1}^{k}$ 꼴로 바꿔도 상관없다.
$\frac{1}{6}$ 으로 정리하자.
$\sum\limits_{i=1}^{k} i^2 = \frac{1}{6}[2(k + 1)^3 - 3k(k + 1) - 2(k + 1)]$
$\bf {y = \frac{x^2}{2}}$ 적분

$\bf {y = \frac{x^2}{2}}$
다시 돌아와서, 이제 위 그래프의 넓이를 구할 수 있게 되었다.
사실 이렇게 넓이 구하는게 적분이라고 한다.
이제 아까 구한 식을 $\sum\limits_{k=1}^{n} k^2$에 대입.
$
\large
\lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \sum\limits_{k=1}^{n} k^2
$
$ \large \lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \frac{1}{6}[2(n + 1)^3 - 3n(n + 1) - 2(n + 1)] $
일단 괄호를 다 풀자.
$
\large
\lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \frac{1}{6}[2n^3 + 6n^2 + 6n + 2 - 3n^2 + 3n - 2n - 2]
$
n은 극한이므로 최고차항만 남기면 된다.
$
\large
\lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \frac{1}{6}[2n^3]
$
$
\large
\lim\limits_{n \to \infty} \ \frac{x^3}{2n^3} \cdot \frac{2n^3}{6}
$
$
\large
\lim\limits_{n \to \infty} \ \frac{x^3}{6}
$
$\large y = \frac{x^2}{2}$ 에 대한 적분은 $\large \frac{x^3}{6}$ 이다.
$\bf {y = \frac{x^3}{6}}$ 적분
우리는 이자에 대한 이자에 대한 이자… 를 구해야 하므로 이를 다시 적분해보자.
똑같이 무수히 많은 직사각형으로 쪼개어 넓이를 구하면 된다.
$
\lim\limits_{n \to \infty} \ \sum\limits_{k=1}^{n} [ \frac{x}{n} \cdot \frac{(k \frac{x}{n})^3}{6} ]
$
$
\lim\limits_{n \to \infty} \ \frac{x^4}{6n^4} \cdot \sum\limits_{k=1}^{n} k^3
$
이젠 또 $\sum\limits_{k=1}^{n} k^3$을 구해야 하는데,
아까 구한 $\sum\limits_{k=1}^{n} k^2$와 비슷하게 구하면 된다.
똑같이 $\sum\limits_{k=1}^{n} k^3$ 는 4차식으로 표현할 수 있을 것이라 생각하고,
$\sum\limits_{k=1}^{n} k^4$ 형식에서 유도한다.
$\sum\limits_{i=0}^{k} [(i + 1)^4 - i^4]$
자 여기서 시작하자.
이걸 똑같이 주르륵 적어보면 $(k + 1)^4$ 가 남는다.
그리고 $(i + 1)^4 - i^4 = 4i^3 + 6i^2 + 4i + 1$ 이므로, 다음과 같이 치환할 수 있다.
$
\sum\limits_{i=0}^{k} [(i + 1)^4 - i^4] = 4\sum\limits_{i=0}^{k} i^3 + 6\sum\limits_{i=0}^{k} i^2 + 4\sum\limits_{i=0}^{k} i + \sum\limits_{i=0}^{k} 1 = (k + 1)^4
$
$\sum\limits_{i=0}^{k} i^3$ 을 좌변에 두고 나머지를 우변으로 옮기면,
$\sum\limits_{i=0}^{k} i^3 = \frac{1}{4}[(k + 1)^4 - 6\sum\limits_{i=0}^{k} i^2 - 4\sum\limits_{i=0}^{k} i - (k + 1)]$ 이다.
$\sum\limits_{i=0}^{k} i^2$ 는 아까 구한 것을 대입하고,
$\sum\limits_{i=0}^{k} i$ 는 가우스 합으로,
$\sum\limits_{i=0}^{k} 1$ 은 $k + 1$ 으로 대입한다.
$
\sum\limits_{i=0}^{k} i^3 = \frac{1}{4}[(k + 1)^4 - [2(k + 1)^3 - 3k(k + 1) - 2(k + 1)] - 4\frac{k(k + 1)}{2} - (k + 1)]
$
$
\sum\limits_{i=0}^{k} i^3 = \frac{1}{8}[2(k + 1)^4 - 4(k + 1)^3 + 6k(k + 1) + 4(k + 1) - 4k(k + 1) - 2(k + 1)]
$
어차피 최고차항만 남기면 되므로,
4차항만 남기면 된다.
$
\sum\limits_{i=1}^{k} i^3 = \frac{1}{8}[2(k + 1)^4]
$
$\bf {y = \frac{x^3}{6}}$ 적분
$
\Large
\lim\limits_{n \to \infty} \ \frac{x^4}{6n^4} \cdot \sum\limits_{k=1}^{n} k^3
$
이제 $\sum\limits_{k=1}^{n} k^3$를 구했으니 대입하자.
$
\lim\limits_{n \to \infty} \ \frac{x^4}{6n^4} \cdot \frac{1}{8} \cdot 2(n + 1)^4
$
$
\lim\limits_{n \to \infty} \ \frac{x^4}{6n^4} \cdot \frac{1}{4} \cdot (n + 1)^4
$
$
\lim\limits_{n \to \infty} \ \frac{x^4}{24n^4} \cdot n^4 + 4n^3 + 6n^2 + 4n + 1
$
최고 차항만 남기고 약분.
$
\lim\limits_{n \to \infty} \ \frac{x^4}{24n^4} \cdot n^4
$
$
\lim\limits_{n \to \infty} \ \frac{x^4}{24}
$
$\large y = \frac{x^3}{6}$ 에 대한 적분은 $\large \frac{x^4}{24}$ 이다.
$e$ 정리
이때까지 구한 것을 정리하면 다음과 같다.
$
\large
e = 1 + 1 + \frac{x}{1} + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + …
$
적분을 반복할 때마다 $x$의 차수가 1씩 증가하고,
$x^n$을 적분할 때 필요한 $\sum\limits_{k=1}^{n} k^{n} $은 $\sum\limits_{k=1}^{n} k^{n+1} $을 이용하여 구할 수 있었는데,
이 때 $\sum\limits_{k=1}^{n} k^{n+1} $를 유도하는 과정에서
$(k + 1)^{n+1} - k^{n+1}$ 는 ${ (n+1) \cdot k^n + … + … }$ 꼴로 풀리는 것을 알 수 있었다.
그러므로
$
\lim\limits_{n \to \infty} \ \frac{x^4}{6n^4} \cdot \sum\limits_{k=1}^{n} k^3
$
다음과 같은 적분을 계산할 때,
$\sum\limits_{k=1}^{n} k^3$ 은 $\frac{1}{4} \cdot n^{4}$ 꼴로 계산된다.
이를 일반화하면, $\sum\limits_{k=1}^{n} k^d$ 은 $\frac{1}{d + 1} \cdot n^{d+1}$ 꼴로 계산된다는 것이다.
그렇다면
$\large\frac{x^d}{a}$를 적분하면 $\large\frac{x^{d+1}}{a(d+1)}$ 이 될 것이고,
이는 $\large\frac{x^{d+1}}{(d+1)!}$ 이 될 것이다.
그러므로 이를 $e$ 식에 대입하면,
$
e \ = 1 + 1 + \frac{x}{1} + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + …
$
$
\quad = 1 + 1 + \frac{x}{1!} + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + …
\
$
최종적으로 $e$는 다음과 같이 유도된다.
$
\Large
e^x = \lim\limits_{n \to \infty} \sum\limits_{i=0}^{n} \frac{x^i}{i!}
$
적분과 미분과의 관계
$\frac{x^3}{6}$을 적분하면 $\frac{x^4}{24}$ 이 되었는데,
거꾸로 $\frac{x^4}{24}$를 미분해보자.
$\frac{x^4}{24}$에서 지수를 내리면 $\frac{4x^3}{24}$, 약분하면 $\frac{x^3}{6}$ 이 된다.
$\frac{x^3}{6}$를 적분하면 $\frac{x^4}{24}$, $\frac{x^4}{24}$를 미분하면 $\frac{x^3}{6}$ 이 되는 것이다!!
이를 이용해 $\frac{x^4}{24}$를 적분한 식 $X$를 구할 때,
$X$ 라는 식을 미분한 결과가 $\frac{x^4}{24}$ 이 되는 $X$를 찾아도 된다.
$X$는 $\frac{x^d}{m}$ 꼴일 것인데,
미분하면 지수가 1 내려와 $x^4$가 되어야 하므로 $\frac{x^5}{m}$일 것이고,
지수가 내려오면 $\frac{5x^4}{m}$일 것인데 약분되어 $\frac{x^4}{24}$가 되어야 하므로,
$\frac{x^5}{120}$ 일 것이다.
이것들을 보면, 적분은 미분의 역연산이라고 할 수 있을 것 같다.
(정확히는 적분은 부정적분과 정적분으로 나뉘고 부정적분이 미분의 역연산이라고 하는데,
우리는 부정적분인데 적분상수를 무시한 케이스…? 잘 모르겠다;;)
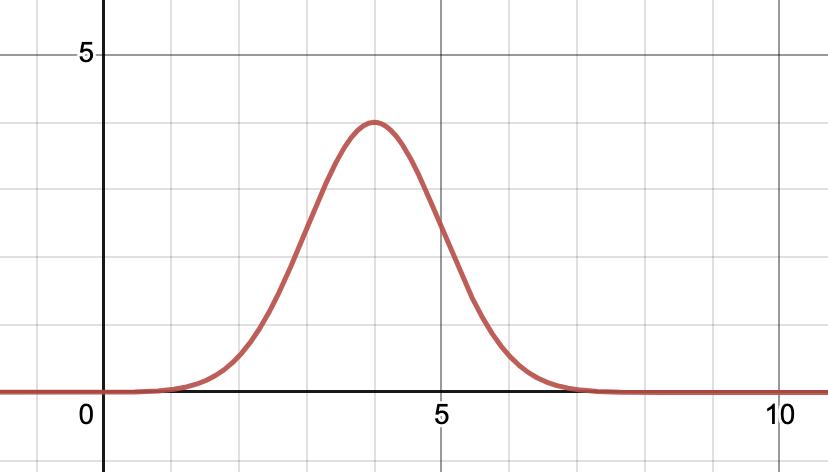
좀 더 직관적으로 생각해보자면 속도함수와 거리함수의 관계를 생각할 수 있을 것 같다.
위 그래프를 어떠한 물체가 이동한 속도에 대한 그래프라고 생각하자.
세로축 y는 속도, 가로축 x는 시간이다.
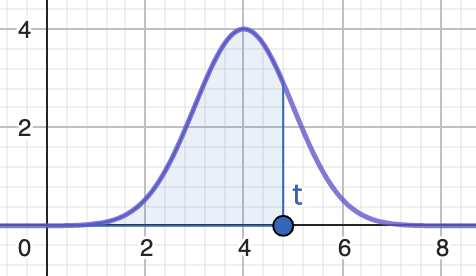
그렇다면 여기서 어떠한 시간 시점 t까지 이동한 거리를 구하려면,
범위 0부터 t까지 속도함수의 넓이를 구하면 된다.
즉 적분이다.
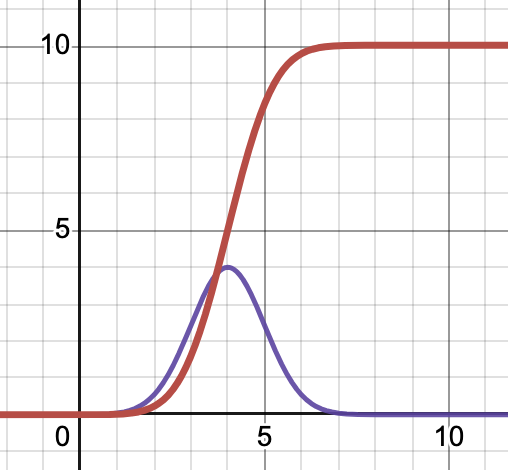
이로 구한 거리함수는 다음과 같다.
이 거리함수의 각 지점 기울기에 대한 함수를 구하면,
다시 속도함수가 될 것이다.
Natural log : $ln(x)$
이제 자연로그를 정의할 수 있다.
$e^x$에 대하여 정의하였으므로,
$ln(e^x) = x$로 정의할 수 있다.
$ln(x)$를 미분하면 어떻게 될까?
$y = ln(x)$ 라고 생각해보자.
이러면 $e^y = x$ 가 되고,
이걸 양 변을 x로 미분하자.
$\frac{d}{dx} e^y = \frac{d}{dx} x$,
$e$의 특성상 $e^y$를 $y$로 미분하면 그대로 $e^y$가 되므로,
chain rule로
$e^y \cdot \frac{dy}{dx} = \frac{d}{dx}x$
$\frac{d}{dx}x$는 자기 자신이니까 1.
$e^y \cdot \frac{dy}{dx} = 1$
$\frac{dy}{dx} = \frac{1}{e^y}$
$\frac{dy}{dx} = \frac{1}{e^{ln(x)}}$
$\frac{dy}{dx} = \frac{1}{x}$
미분은 $\frac{1}{x}$가 된다.
$e$의 미분
$e$가 재밌는 점은, $e$를 미분하였을 때 자기 자신이 나온다는 것이다.
직접 미분해보자.
$ e^x = 1 + \frac{x^1}{1} + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + … $
1을 미분하면 0,
x를 미분하면 1,
$\frac{x^2}{2}$를 미분하면 $\frac{2x}{2}$, 약분되므로 $\frac{x}{1}$,
$\frac{x^3}{6}$을 미분하면 $\frac{3x^2}{6}$, 약분되므로 $\frac{x^2}{2}$,
이를 무한히 반복하므로 미분도 결국 자기 자신이 된다.
$
\frac{d}{dx} e^x = 0 + 1 + \frac{x}{1} + \frac{x^2}{2} + \frac{x^3}{6} + \frac{x^4}{24} + …
$
